Must-See Stories & Smart Solutions

The Rosetta Stone of Intelligent Buildings
Does your organization struggle with internal projects because teams aren’t on the same page?
Let's Walk the Talk: Newcomb & Boyd's Sustainability Journey
Newcomb & Boyd’s newly renovated Atlanta Office provides a space that is comfortable, healthy, and sustainable for employees and visitors. Following the company mission and values, the new office incorporates design features focused on sustainability and wellness for employees.


Taking Junction Krog District to LEED Gold
Junction Krog District initially set out to achieve LEED v4 Core and Shell certification at the Certified Level. Through our innovative pilot approaches in energy and water analyses, we gained additional points, surpassing standard documentation pathways. Without incurring any additional costs or requiring extensive design modifications, the collaborative endeavors of our team not only met but exceeded the objective, and the project achieved LEED Gold certification.
Cybersecurity Operational Technology Services
Our cybersecurity services offer a comprehensive approach to safeguarding your operational technologies. We enhance cybersecurity awareness through educational programs and create customized frameworks for risk management and asset security. Here’s how we can support you:

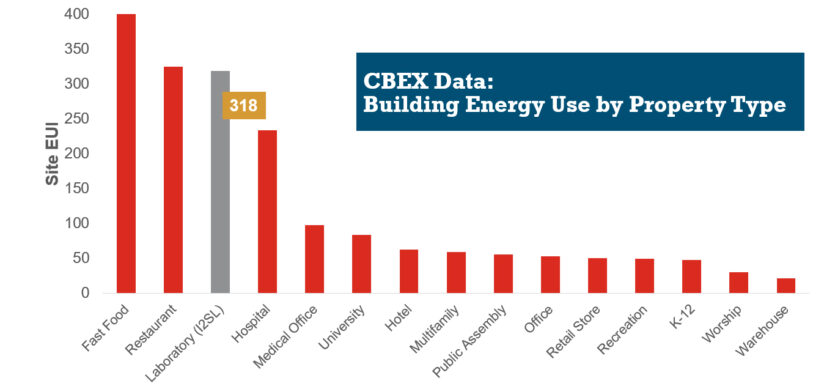
HVAC Design Approaches for Sustainable Laboratories
HVAC systems in a typical laboratory facility can use five to 10 times as much energy as the systems in a typical office building. This higher energy use is due to many factors, including 100 percent outside air systems, 24-hour-a-day operation, high internal heat gains, high air change rate requirements, equipment exhaust requirements, and high fan energy. With this significant energy use, the incentive for creative sustainable design grows—not only to create forward-thinking research spaces, but to maximize a lab’s ROI.